「原作者へ」
連絡先を存じ上げませんでしたので、不本意ながら無断で翻訳しました。
正式に翻訳を許可されたいです。
gogyzzz@gmail.comでご連絡ください。
아래 포스트의 번역입니다.
http://work-in-progress.hatenablog.com/entry/2018/10/06/124604
파라미터 업데이트의 과정에서 하고 있는 것은 「Natural Gradient for Stochastic Gradient Descent (NG-SGD)」이라는 이름이 붙어있다.
용어의 복습
「Stochastic Gradient Descent」는 shuffle한 학습 데이터로 gradient를 계산, 파라미터 업데이트를 반복하는 방법. 하나의 학습 데이터를 사용하는 것이 온라인 학습, 여러개의 학습 데이터를 사용하는 것이 미니배치 학습.
「Natural Gradient method」는 그들 연구에서 쓰이는 용어로 fisher information 행렬의 역행렬(근사)을 learning rate matrix(???)로서 사용하는 방법이다.
previous work has used the term “Natural Gradient” to describe methods like ours which use an approximated inverse-Fisher matrix as the learning rate matrix, so we follow their precedent in calling our method “Natural Gradient”.
핵심이 되는 계산은 N행으로 구성된 행렬 X가 있을 때 i번째의 행 벡터 「xi」에 fisher information (Fi)의 역수를 곱하는 것이다.

여기에서 fisher information「Fi」은 i번째의 행을 뺀 다른 행「xj」으로부터 구할 수 있다.

이 아이디어를 기반으로, 아래 2개의 확장을 추가했다고 한다.
- smoothing of Fi with the identity matrix (단위 행렬에 의한 Fi의 equalization)
- scaling the output to have the same Frobenius norm as the input(input과 같은 frobenius norm을 가지도록 output을 스케일링)
여기서, N행 x D열의 행렬 「Xt」가 있을 때 「Xt」를 column-wise(열 방향)으로 생각하면 fisher information matrix 「F_i」은 D행 x D열이 된다(X^T X)
fisher information matrix를 R차원의 낮은 랭크로 근사하여,

t : 미니배치 index
F_t : D행 x D열
R_t : R행 x D행
D_t : R행 x R행
I : D행 x D열、identity matrix (단위행렬)
rhot : 0 < rhot
역행렬 (근사한 것)을 구한다.


G_t : D행 x D열
E_t : R행 x R행
beta_t : scalar
column-wise(열방향)이므로, 곱셈은 「Xt」의 우측에서 곱하여 「Xt」을 업데이트한다.

이는 이전 글의 아래 부분에 해당한다.

이어서 스케일링.

이 부분은 이전 글의 「gamma_t」에 해당한다.

좀 더 자세히 보도록 하자.
업데이트 대상인 파라미터의 차원(D)가 376, 미니배치 사이즈(N)이 128, 낮은 랭크로 근사한 차원(R)이 30이라 하자.
행렬 X_t(N행 x D열)은, transpose 행렬을 곱하여 대칭행렬로 만든 후 계산한다.
또한 논문에서는
파라미터의 차원(D) < 미니배치의 차원(N)
을 상정하여 column-wise(열방향)으로 되어 있다.
(학습이 진행됨에 따라, 미니배치 사이즈는 점점 커진다(예를 들어 512))
계산은 D차원(=full-rank)의 대칭행렬 「T_t」(D행 x D열)에 대해서가 아니라,

S_t : D행 x D열

eta : forgetting factor、0 < η < 1
R차원(=row-rank approximation)의 대칭행렬 「Z_t」(R행 x R열)에 대해 수행한다.

Y_t : R행 x D열
R_t : R행 x D행
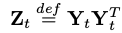
위의 「Rt」을 스케일링 한것을 「Wt」로 두어,

W_t : R행 x D행
이것을 weight 행렬로써 적절한 값이 되도록 업데이트하는 것이 목적이 된다.
일단은 「R_t」를 초기화하자.
이것은 R차원의 직교행렬을 가로로 늘어놓은 형태가 된다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::InitDefault()
// after the next line, W_t_ will store the orthogonal matrix R_t.
InitOrthonormalSpecial(&W_t_);
R_t (R x D)

「E_t」의 초기값을 구하여, 그것의 root를 곱한다.
BaseFloat E_tii = 1.0 / ( 2.0 + (D + rank_) * alpha_ / D );
// W_t =(def) E_t^{0.5} R_t.
W_t_.Scale(sqrt(E_tii));
다음의 미니배치에 대해 「W_t」를 업데이트한다.
업데이트 식은 아래와 같다.

W_t1 : R행 x D열
E_t1 : R행 x R행、diagonal matrix
R_t1 : R행 x D열
C_t : R행 x R행、diagonal matrix
U_t : R행 x R열、Orthogonal matrix
Y_t : R행 x D열
J_t : R행 x D열
D_t : R행 x R행
eta : forgetting factor、0 < η < 1
「Ut」(직교행렬)와 「Ct」(특이값)은, 「Z_t」를 SVD하여 얻는다.

아래 「Z_t」를 구하는 과정
원래의 input 「Xt」(N행 x D열)에, 「Wt」(R행 x D열)의 전치행렬을 오른쪽에서부터 곱하여, 「H_t」(N행 x R열)을 구한다(「N」은 미니배치사이즈)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
H_t.AddMatMat(1.0, *X_t, kNoTrans, W_t, kTrans, 0.0); // H_t = X_t W_t^T
H_t (N x R)

열 수 「D」(376차원)의 input (X_t)가, 열 수「R」(30차원)의 행렬이 된다.
이어서, 「J_t」를 구한다.
원래의 input 「Xt」(N행 x D열)에 「Ht」(N행 x R열)의 전치행렬을 왼쪽에서부터 곱하여 「J_t」(R행 x D열)을 구한다.
(「W_t」와 같은 행 수, 열 수가 된다)
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
J_t.AddMatMat(1.0, H_t, kTrans, *X_t, kNoTrans, 0.0); // J_t = H_t^T X_t
「J_t」의 식을 변형하면
J_t = H_t^T X_t
= (X_t W_t^T)^T X_t
= W_t X_t^T X_t
「X_t」(N행 x D열)의 「uncentered covariance matrix」(D행 x D열)에, Weight Matrix(R행 x D열)를 왼쪽에서 곱한 것이라고 할 수도 있다.
J_t (R x D)

이어서 「K_t」를 구한다.
「J_t」(R행 x D열)에 대하여, 전치행렬을 오른쪽에서부터 곱한 것에 해당한다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
K_t.SymAddMat2(1.0, J_t, kNoTrans, 0.0); // K_t = J_t J_t^T
K_t (R x R、symmetric)

이어서 「L_t」을 구한다.
「H_t」(N행 x R열)에 대해, 전치행렬을 왼쪽에서 곱한 것에 해당한다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
L_t.SymAddMat2(1.0, H_t, kTrans, 0.0); // L_t = H_t^T H_t
L_t (R x R、symmetric)

「Kt」과 「Lt」을 사용하여, 「Z_t」를 구한다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
SpMatrix<double> Z_t_double(R);
ComputeZt(N, rho_t, d_t, inv_sqrt_e_t, K_t_cpu, L_t_cpu, &Z_t_double);
Z_t (R x R、symmetric)

스케일 변환 후, SVD한다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
Matrix<BaseFloat> U_t(R, R);
Vector<BaseFloat> c_t(R);
// do the symmetric eigenvalue decomposition Z_t = U_t C_t U_t^T.
Z_t_scaled.Eig(&c_t, &U_t);
SortSvd(&c_t, &U_t);
c_t.Scale(z_t_scale);
C_t (30차원)
0.957 0.164 0.119 0.090 ... 0.00019 0.00016
U_t (R x R)

「W_t」를 업데이트한다.

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::PreconditionDirectionsInternal()
CuMatrix<BaseFloat> W_t1(R, D); // W_{t+1}
ComputeWt1(N,
d_t,
d_t1,
rho_t,
rho_t1,
U_t,
sqrt_c_t,
inv_sqrt_e_t,
W_t,
&J_t,
&W_t1);
「B_t」를 구한다.
B_t (R x D)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// B_t = J_t + (1-eta)/(eta/N) (D_t + rho_t I) W_t
J_t->AddDiagVecMat(1.0, w_t_coeff_gpu, W_t, kNoTrans, 1.0);
wtcoeffgpu : R행 x R행, 대각행렬, Wt의 각 행에 대한 계수
식의 변형은 아래와 같다.
B_t = J_t + ( W_t계수 * W_t )
= ( W_t X_t^T X_t ) + ( W_t계수 * W_t )
「A_t」를 구한다.
A_t (R x R)

[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// A_t = (eta/N) E_{t+1}^{0.5} C_t^{-0.5} U_t^T E_t^{-0.5} B_t
Matrix<BaseFloat> A_t(U_t, kTrans);
for (int32 i = 0; i < R; i++) {
BaseFloat i_factor = (eta / N) * sqrt_e_t1(i) * inv_sqrt_c_t(i);
for (int32 j = 0; j < R; j++) {
BaseFloat j_factor = inv_sqrt_e_t(j);
A_t(i, j) *= i_factor * j_factor;
}
}
「W_t1」를 구한다.
[ nnet2/nnet-precondition-online.cc ] OnlinePreconditioner::ComputeWt1()
// W_{t+1} = A_t B_t
CuMatrix<BaseFloat> A_t_gpu(A_t);
W_t1->AddMatMat(1.0, A_t_gpu, kNoTrans, *J_t, kNoTrans, 0.0);
「Wt1」를 사용하여 「Xt」를 업데이트한다.

이것을 반복하여, 업데이트 된 「Xt」는 이전 글에서 보았던 「invaluetemp」、「outderiv_temp」에 해당한다.
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
preconditioner_in_.PreconditionDirections(&in_value_temp,
&in_row_products,
&in_scale);
preconditioner_out_.PreconditionDirections(&out_deriv_temp,
&out_row_products,
&out_scale);
파라미터를 수정하는 벡터로 사용하여 모델의 파라미터를 업데이트.
[ nnet2/nnet-component.cc ] AffineComponentPreconditionedOnline::Update()
bias_params_.AddMatVec(local_lrate, out_deriv_temp, kTrans, precon_ones, 1.0);
linear_params_.AddMatMat(local_lrate, out_deriv_temp, kTrans, in_value_precon_part, kNoTrans, 1.0);







